Data Science 2025 / Final Project¶
Studiying the borns and deaths os my country, Spain, takins several data from the Intituto Nacional de Estadistica (nacional agency os statistics) and see how well our country is developing in keeping the population and life expectancy. Data from here: https://www.epdata.es/datos/nacimientos-muertes-estadisticas-graficos-datos-ine/67/espana/106
THE DATA¶
#first of all lets see what we have in the file
import pandas as pd
df = pd.read_json('datasets/nacimientos_espana_1975_2024.json')
print(df)
year births 0 1975 677456 1 1976 657828 2 1977 640494 3 1978 634226 4 1979 618654 5 1980 571018 6 1981 545530 7 1982 531463 8 1983 518163 9 1984 502426 10 1985 494314 11 1986 482891 12 1987 474624 13 1988 475421 14 1989 401108 15 1990 403386 16 1991 396747 17 1992 384830 18 1993 362626 19 1994 360471 20 1995 363469 21 1996 362626 22 1997 362193 23 1998 365193 24 1999 389357 25 2000 396626 26 2001 405313 27 2002 417688 28 2003 440531 29 2004 453172 30 2005 464811 31 2006 482954 32 2007 518032 33 2008 519779 34 2009 494997 35 2010 485252 36 2011 471999 37 2012 454648 38 2013 425715 39 2014 426303 40 2015 419109 41 2016 408384 42 2017 391930 43 2018 372777 44 2019 360617 45 2020 339206 46 2021 338532 47 2022 329251 48 2023 322075 49 2024 321500
i find two data columns: year and births. Lets make a Graph about the births in the country os spain, by number. Just a simple scatter and plotting the data:
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_json('datasets/nacimientos_espana_1975_2024.json')
df.plot(kind = 'scatter', x = 'year', y = 'births')
plt.show()
I can see there is a enourmous number of borns in the 75 years (we call here Baby boom) because of the end of the dictatorship era. After this boom the borns goes down until year 98, the a little rise up until year 2008 (when the lehman brothers affaire) and then going down.
df['births'].plot.kde()
<Axes: ylabel='Density'>
I also want to check the data of deaths in Spain in the same time split. You can find the data here: https://www.epdata.es/defunciones-ocurridas-espana-1900/d1fec921-3674-4e24-895c-7251f8f9cb10
df2 = pd.read_csv('datasets/deaths_year.csv')
print(df2)
year deaths 0 1975 298192 1 1976 299007 2 1977 294324 3 1978 296781 4 1979 291213 5 1980 289344 6 1981 293386 7 1982 286655 8 1983 302569 9 1984 299409 10 1985 312532 11 1986 310413 12 1987 310073 13 1988 319437 14 1989 324796 15 1990 333142 16 1991 337691 17 1992 331515 18 1993 339661 19 1994 338242 20 1995 346227 21 1996 351449 22 1997 349521 23 1998 360511 24 1999 371102 25 2000 360391 26 2001 360131 27 2002 368618 28 2003 384828 29 2004 371934 30 2005 387355 31 2006 371478 32 2007 385361 33 2008 386324 34 2009 384933 35 2010 382047 36 2011 387911 37 2012 402950 38 2013 390419 39 2014 395830 40 2015 422568 41 2016 410611 42 2017 424523 43 2018 427721 44 2019 418703 45 2020 493776 46 2021 450744 47 2022 463133 48 2023 436124 49 2024 433547
Now i have to do the same with the death by year. Be careful that all data are the same at both datafiles. Unoe column for the year, and the other column with data without dots
df2.plot(kind = 'scatter', x = 'year', y = 'deaths')
plt.show()
df2['deaths'].plot.kde()
<Axes: ylabel='Density'>
Now i want to mix both data (births and deaths) in the same graphic:
plt.plot(df["year"], df["births"], label="Births")
plt.plot(df2["year"], df2["deaths"], label="Deaths")
plt.legend()
plt.show()
THE FITTING¶
Now, having this two data in the plot, lets try to find the best fitting form to this data. As i see the deaths will be easy, because it slightly grow up in time. But the births has a more complex form, goes down, then rise a little bit and then goes down again .So it seems that the deaths has a deg 2 polinomial and the births are deg3.
Using numpy to find this polinoms:
import numpy as np
# load data
year_b, births = df["year"].values, df["births"].values
year_d, deaths = df2["year"].values, df2["deaths"].values
# adjusting polinomies
coef_births = np.polyfit(year_b, births, deg=3)
coef_deaths = np.polyfit(year_d, deaths, deg=2)
poly_births = np.poly1d(coef_births)
poly_deaths = np.poly1d(coef_deaths)
# common range
years = np.linspace(1975, max(year_b.max(), year_d.max()), 300)
plt.plot(year_b, births, "o", alpha=0.4, label="Births (data)")
plt.plot(years, poly_births(years), "-", label="Births fit (deg 3)")
plt.plot(year_d, deaths, "o", alpha=0.4, label="Deaths (data)")
plt.plot(years, poly_deaths(years), "-", label="Deaths fit (deg 2)")
plt.legend()
plt.xlabel("Year")
plt.ylabel("Count")
plt.title("Polynomial fitting: births vs deaths (Spain)")
plt.show()
Overall, this fitting approach provides a reasonable approximation of the long-term demographic trends and allows for a clear comparison between both series.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# load data
X = df["year"].values.reshape(-1, 1)
y = df["births"].values
# ML model: polinomial regression
degree = 3 # same deg that i find in the fitting
model = make_pipeline(
PolynomialFeatures(degree=degree),
LinearRegression()
)
# train model
model.fit(X, y)
#prediction
years = np.linspace(X.min(), X.max(), 300).reshape(-1, 1)
y_pred = model.predict(years)
#visualization
plt.figure(figsize=(8,5))
plt.scatter(X, y, label="Births (data)", alpha=0.6)
plt.plot(years, y_pred, color="red", label=f"Polynomial regression (deg {degree})")
plt.xlabel("Year")
plt.ylabel("Births")
plt.title("Polynomial Regression with scikit-learn")
plt.legend()
plt.grid(True)
plt.show()
THE MACHINE LEARNING¶
Checking the resoluts in the ML approximation data:
from sklearn.metrics import mean_squared_error, r2_score
y_fit = model.predict(X)
mse = mean_squared_error(y, y_fit)
r2 = r2_score(y, y_fit)
print(f"MSE: {mse:.2e}")
print(f"R²: {r2:.4f}")
MSE: 1.03e+09 R²: 0.8742
The results its not great (must be closer to 1) but there are not so much data to work on. Pretty close to a nice result. Im going to use the same approximation with deaths data:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# load data
X = df2["year"].values.reshape(-1, 1)
y = df2["deaths"].values
# ML model: polinomial regression
degree = 2 # same deg that i find in the fitting
model = make_pipeline(
PolynomialFeatures(degree=degree),
LinearRegression()
)
# train model
model.fit(X, y)
#prediction
years = np.linspace(X.min(), X.max(), 300).reshape(-1, 1)
y_pred = model.predict(years)
#visualization
plt.figure(figsize=(8,5))
plt.scatter(X, y, label="Deaths (data)", alpha=0.6)
plt.plot(years, y_pred, color="red", label=f"Polynomial regression (deg {degree})")
plt.xlabel("Year")
plt.ylabel("Deaths")
plt.title("Polynomial Regression with scikit-learn")
plt.legend()
plt.grid(True)
plt.show()
THE PROBABILITY¶
Now lets find the probability distribution of births and deaths:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
births = df["births"].values
deaths = df2["deaths"].values
# probability of born
plt.figure(figsize=(8,5))
plt.hist(births, bins=15, density=True, alpha=0.5, label="Births (data)")
mu_b, sigma_b = norm.fit(births)
x = np.linspace(births.min(), births.max(), 300)
plt.plot(x, norm.pdf(x, mu_b, sigma_b), "r-",
label=f"Normal fit μ={mu_b:.0f}, σ={sigma_b:.0f}")
plt.title("Probability distribution of annual births (Spain)")
plt.xlabel("Number of births per year")
plt.ylabel("Probability density")
plt.legend()
plt.grid(True)
plt.show()
plt.figure(figsize=(8,5))
plt.hist(deaths, bins=15, density=True, alpha=0.5, label="Deaths (data)")
mu_d, sigma_d = norm.fit(deaths)
x = np.linspace(deaths.min(), deaths.max(), 300)
plt.plot(x, norm.pdf(x, mu_d, sigma_d), "g-",
label=f"Normal fit μ={mu_d:.0f}, σ={sigma_d:.0f}")
plt.title("Probability distribution of annual deaths (Spain)")
plt.xlabel("Number of deaths per year")
plt.ylabel("Probability density")
plt.legend()
plt.grid(True)
plt.show()
With that we can see some probability data realted with this numbers:
threshold = 350_000
prob = norm.cdf(threshold, mu_b, sigma_b)
print(f"Probability(births < {threshold}) = {prob:.2f}")
Probability(births < 350000) = 0.14
threshold = 450_000
prob = 1 - norm.cdf(threshold, mu_d, sigma_d)
print(f"Probability(deaths > {threshold}) = {prob:.2f}")
P(deaths > 450000) = 0.04
THE DENSITY ESTIMATION¶
Analyzing the probability distribution of annual births and deaths in Spain by treating the yearly values as realizations of random variables. Histograms and kernel density estimates were used to visualize the empirical distributions, and normal distributions were fitted to each dataset. The fitted parameters provide an estimate of the typical annual values and their variability, while extreme years appear as low-probability events in the tails of the distributions.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from sklearn.mixture import GaussianMixture
import seaborn as sns
births = df["births"].values
deaths = df2["deaths"].values
#KDE vs normal
plt.figure(figsize=(8,5))
# Histogram
plt.hist(births, bins=15, density=True, alpha=0.4, label="Births (data)")
# KDE
sns.kdeplot(births, linewidth=2, label="KDE")
# Normal
mu_b, sigma_b = norm.fit(births)
x = np.linspace(births.min(), births.max(), 300)
plt.plot(x, norm.pdf(x, mu_b, sigma_b), "r--", label="Normal fit")
plt.title("Density estimation of annual births (Spain)")
plt.xlabel("Number of births per year")
plt.ylabel("Density")
plt.legend()
plt.grid(True)
plt.show()
KDE follows better the asymetry of data in this case, and the normal soften too much tha data.
plt.figure(figsize=(8,5))
plt.hist(deaths, bins=15, density=True, alpha=0.4, label="Deaths (data)")
sns.kdeplot(deaths, linewidth=2, label="KDE")
mu_d, sigma_d = norm.fit(deaths)
x = np.linspace(deaths.min(), deaths.max(), 300)
plt.plot(x, norm.pdf(x, mu_d, sigma_d), "g--", label="Normal fit")
plt.title("Density estimation of annual deaths (Spain)")
plt.xlabel("Number of deaths per year")
plt.ylabel("Density")
plt.legend()
plt.grid(True)
plt.show()
births_reshaped = births.reshape(-1, 1)
gmm_b = GaussianMixture(n_components=2, random_state=0)
gmm_b.fit(births_reshaped)
means_b = gmm_b.means_.flatten()
stds_b = np.sqrt(gmm_b.covariances_.flatten())
weights_b = gmm_b.weights_.flatten()
print("GMM Births:")
for i in range(2):
print(f"Component {i+1}: μ={means_b[i]:.0f}, σ={stds_b[i]:.0f}, weight={weights_b[i]:.2f}")
GMM Births: Component 1: μ=381361, σ=36732, weight=0.46 Component 2: μ=506313, σ=82932, weight=0.54
x = np.linspace(births.min(), births.max(), 300)
logprob = gmm_b.score_samples(x.reshape(-1,1))
pdf_gmm = np.exp(logprob)
plt.figure(figsize=(8,5))
plt.hist(births, bins=15, density=True, alpha=0.4, label="Data")
plt.plot(x, pdf_gmm, "k-", label="GMM total")
for i in range(2):
plt.plot(
x,
weights_b[i] * norm.pdf(x, means_b[i], stds_b[i]),
"--",
label=f"Component {i+1}"
)
plt.title("GMM density estimation – Births")
plt.legend()
plt.grid(True)
plt.show()
Detects two components: one component is the years where there are a lot of newborns and the other component are the years with low births
CONCLUSION¶
In this project, i analyzed long-term demographic data for Spain, focusing on annual births and deaths since 1975.
We first explored the data visually and applied polynomial fitting to model the underlying trends. A third-degree polynomial captured the strong non-linear decline in births, while a second-degree polynomial was sufficient to describe the smoother increase in deaths.
I then applied supervised machine learning techniques, using polynomial regression implemented with scikit-learn. The machine learning model produced results comparable to classical fitting while providing a more flexible and extensible framework, including standard evaluation metrics and pipeline-based transformations.
From a probabilistic perspective, i treated the annual values as realizations of random variables and investigated their probability distributions. Density estimation techniques such as Kernel Density Estimation (KDE) and Gaussian Mixture Models (GMM) were used to characterize the variability of the data and to identify different demographic regimes, particularly in the births series.
Overall, the combination of classical fitting, machine learning regression, and density estimation provides a coherent and complementary view of the data. These methods allow me to model long-term trends, assess variability, and identify structural changes in demographic behavior, demonstrating the usefulness of data science techniques for analyzing real-world societal data.
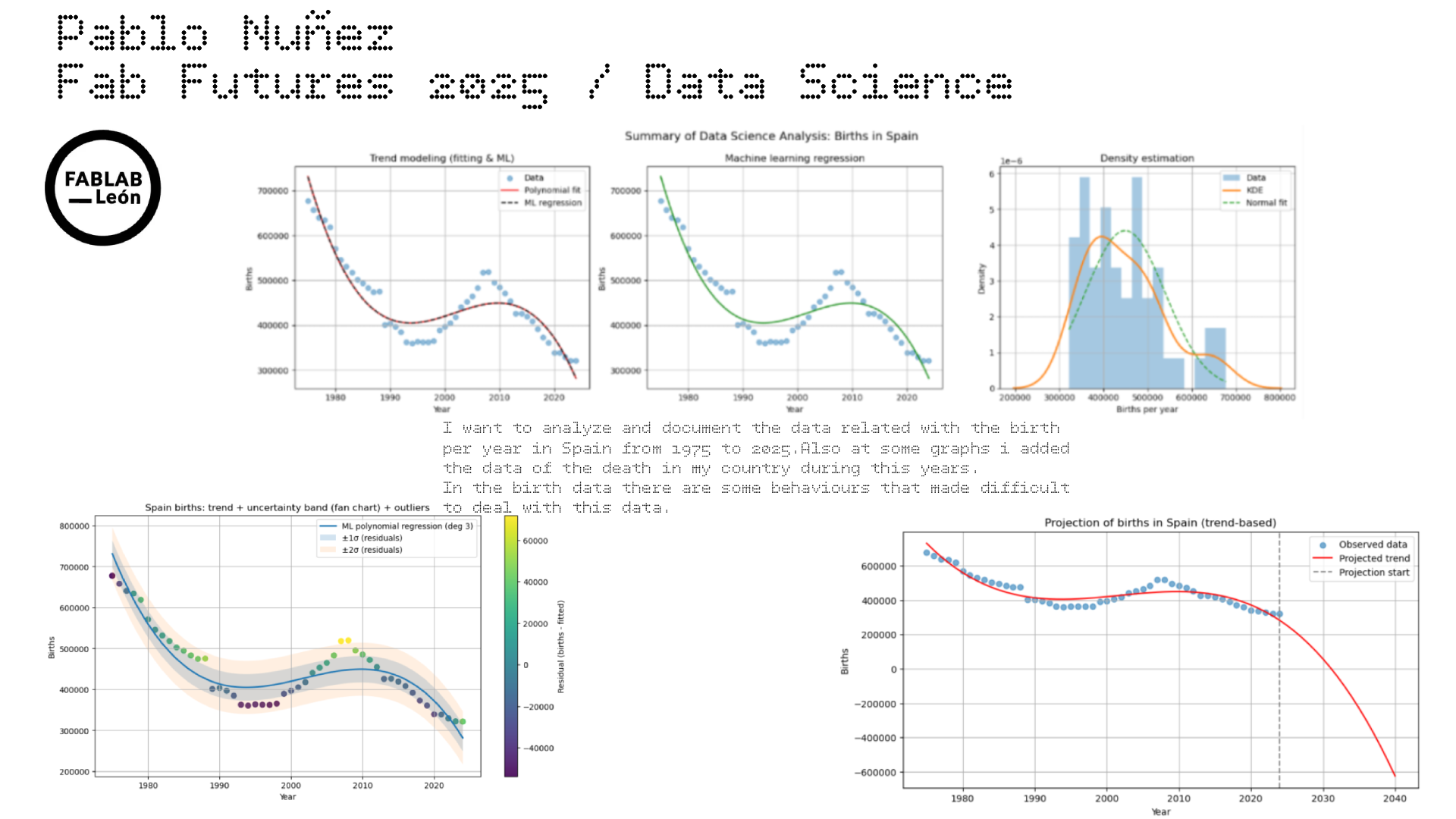
Since the most critical dataset used here is the borns in spain from 75 to 2025, im going to make a resume of the project with three plot seeing the three steps of the investigation: fitting, ML and density estimation
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import seaborn as sns
# data load
years = df["year"].values
births = df["births"].values
X = years.reshape(-1, 1)
y = births
x_plot = np.linspace(years.min(), years.max(), 300).reshape(-1, 1)
# fitting
poly_coef = np.polyfit(years, births, deg=3)
poly_fit = np.poly1d(poly_coef)
# Machine learning with polinomial regression
ml_model = make_pipeline(
PolynomialFeatures(degree=3),
LinearRegression()
)
ml_model.fit(X, y)
y_ml = ml_model.predict(x_plot)
# Density estiamtion
mu, sigma = norm.fit(births)
#resume ploting
fig, axs = plt.subplots(1, 3, figsize=(18, 5))
# --- Subplot 1: Fitting clásico + ML
axs[0].scatter(years, births, alpha=0.5, label="Data")
axs[0].plot(x_plot, poly_fit(x_plot), label="Polynomial fit", color="red")
axs[0].plot(x_plot, y_ml, "--", label="ML regression", color="black")
axs[0].set_title("Trend modeling (fitting & ML)")
axs[0].set_xlabel("Year")
axs[0].set_ylabel("Births")
axs[0].legend()
axs[0].grid(True)
# plot2: ML model only
axs[1].scatter(years, births, alpha=0.5)
axs[1].plot(x_plot, y_ml, color="green")
axs[1].set_title("Machine learning regression")
axs[1].set_xlabel("Year")
axs[1].set_ylabel("Births")
axs[1].grid(True)
# plot3: Density estimation
axs[2].hist(births, bins=15, density=True, alpha=0.4, label="Data")
sns.kdeplot(births, ax=axs[2], linewidth=2, label="KDE")
x = np.linspace(births.min(), births.max(), 300)
axs[2].plot(x, norm.pdf(x, mu, sigma), "--", label="Normal fit")
axs[2].set_title("Density estimation")
axs[2].set_xlabel("Births per year")
axs[2].set_ylabel("Density")
axs[2].legend()
axs[2].grid(True)
plt.suptitle("Summary of Data Science Analysis: Births in Spain", fontsize=14)
plt.tight_layout()
plt.show()
Now lets try to make a more fancy example of the data visualization:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# Datos
years = df["year"].values
births = df["births"].values
X = years.reshape(-1, 1)
# ML polynomial regression (grado 3, como ya usabas)
degree = 3
model = make_pipeline(PolynomialFeatures(degree=degree), LinearRegression())
model.fit(X, births)
# Predicción en años originales y cálculo de residuos
y_hat = model.predict(X)
residuals = births - y_hat
# Estimar "incertidumbre" con la desviación típica de los residuos
sigma = residuals.std(ddof=1)
# Eje suave para la curva
x_plot = np.linspace(years.min(), years.max(), 400)
X_plot = x_plot.reshape(-1, 1)
y_plot = model.predict(X_plot)
# Colorear puntos por residuo (outliers destacan)
plt.figure(figsize=(11,6))
sc = plt.scatter(years, births, c=residuals, s=45, alpha=0.9)
# Curva del modelo
plt.plot(x_plot, y_plot, linewidth=2, label=f"ML polynomial regression (deg {degree})")
# Bandas tipo fan chart: ±1σ y ±2σ
plt.fill_between(x_plot, y_plot - sigma, y_plot + sigma, alpha=0.2, label="±1σ (residuals)")
plt.fill_between(x_plot, y_plot - 2*sigma, y_plot + 2*sigma, alpha=0.12, label="±2σ (residuals)")
plt.colorbar(sc, label="Residual (births - fitted)")
plt.title("Spain births: trend + uncertainty band (fan chart) + outliers")
plt.xlabel("Year")
plt.ylabel("Births")
plt.grid(True)
plt.legend()
plt.show()
Interanual graphic:
import numpy as np
import matplotlib.pyplot as plt
years = df["year"].values
births = df["births"].values
pct_change = 100 * (births[1:] - births[:-1]) / births[:-1]
years_change = years[1:]
plt.figure(figsize=(11,4))
plt.axhline(0, linewidth=1)
plt.bar(years_change, pct_change)
plt.title("Spain births: year-over-year change (%)")
plt.xlabel("Year")
plt.ylabel("% change")
plt.grid(True, axis="y", alpha=0.3)
plt.show()
Adding the deaths by year to this graphic:
import numpy as np
import matplotlib.pyplot as plt
# data load
years_b = df["year"].values
births = df["births"].values
years_d = df2["year"].values
deaths = df2["deaths"].values
# Asegurar mismo rango temporal
years = np.intersect1d(years_b, years_d)
births = df[df["year"].isin(years)]["births"].values
deaths = df2[df2["year"].isin(years)]["deaths"].values
# internaual variation %
births_pct = 100 * (births[1:] - births[:-1]) / births[:-1]
deaths_pct = 100 * (deaths[1:] - deaths[:-1]) / deaths[:-1]
years_pct = years[1:]
#combined graphic
plt.figure(figsize=(11,5))
plt.axhline(0, color="black", linewidth=1)
plt.plot(years_pct, births_pct, label="Births (% change)", linewidth=2)
plt.plot(years_pct, deaths_pct, label="Deaths (% change)", linewidth=2)
plt.title("Year-over-year variation (%) of births and deaths in Spain")
plt.xlabel("Year")
plt.ylabel("Annual change (%)")
plt.legend()
plt.grid(True, axis="y", alpha=0.3)
plt.show()
The future¶
I want to know, based in this data and in the analysis, which could be the next years prediction in the birth of newborns in Spain. The following results should be interpreted as exploratory projections based on historical trends, not as precise forecasts.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# Datos
years = df["year"].values
births = df["births"].values
X = years.reshape(-1, 1)
y = births
# Modelo ML
degree = 3
model = make_pipeline(
PolynomialFeatures(degree=degree),
LinearRegression()
)
model.fit(X, y)
# Proyection until 2040
future_years = np.arange(years.min(), 2041)
X_future = future_years.reshape(-1, 1)
y_future = model.predict(X_future)
#visualization
plt.figure(figsize=(10,5))
plt.scatter(years, births, label="Observed data", alpha=0.6)
plt.plot(future_years, y_future, color="red", label="Projected trend")
#vertical line
plt.axvline(years.max(), linestyle="--", color="gray", label="Projection start")
plt.xlabel("Year")
plt.ylabel("Births")
plt.title("Projection of births in Spain (trend-based)")
plt.legend()
plt.grid(True)
plt.show()
Since the data could be ok, i think this is not taking some consideration (like that will never be negative borns hehe). So maybe this is not a great way to predict the future of birth in Spain